티스토리 뷰
1. 계산 그래프
오차역전파를 이해하기 위해 계산 그래프를 사용한다. 계산 그래프의 이점은 다음과 같다.
- 전체 계산이 아무리 복잡해도, 각 노드에서는 단순한 계산에 집중하여 문제를 단순화할 수 있다.
- 중간 계산 결과를 보관할 수 있다.
- 역전파를 통해 미분을 효율적으로 계산할 수 있다.
2. 연쇄법칙
역전파는 국소적인 미분을 계산 그래프의 오른쪽에서 왼쪽으로 전달하면서 이루어진다. 국소적 미분을 전달하는 원리는 연쇄법칙(chain rule)에 따른 것이다.
연쇄법칙을 설명하려면 합성 함수부터 시작해야 한다. 합성 함수란 여러 함수로 구성된 함수이다. 예를들어 $y=(x+y)^2$는 $z=t^2$와 $t=x+y$ 두 개의 함수가 합성된 형태이다. 연쇄법칙은 합성 함수의 미분에 대한 성질이며, 합성 함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다는 사실이다.
위 식에 적용한다면 ${\partial z \over \partial x} = {\partial z \over \partial t} {\partial t \over \partial x}$이다.
3. 계산 그래프의 역전파
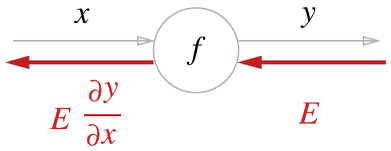
계산 그래프 상에서 역전파의 계산 절차는 상류에서 전달된 값 $E$에 노드의 국소적 미분을 곱한 후 다음 노드로 전달함으로써 진행된다. 이는 연쇄법칙을 그대로 따른 것이다.

예시로 든 합성 함수의 미분을 구하기 위해 계산 그래프에서 역전파를 진행하면 위와 같다.
4. 덧셈 노드의 역전파
$z=x+y$라는 식을 대상으로 덧셈 노드의 역전파가 어떻게 진행되는지 살펴보자. 해당 식의 미분은 ${\partial z \over \partial x} = 1,$ ${\partial z \over \partial y} = 1$이다. 두 값이 모두 1이다.

계산 그래프 상에선, 상류에서 전해진 미분에 1을 곱하여 하류로 흘린다. 즉, 덧셈 노드의 역전파는 1을 곱하기만 할 뿐이므로 입력된 값을 그대로 다음 노드로 보낸다.
5. 곱셈 노드의 역전파
$z=xy$을 생각해보자. 각 변수로 미분해보면 나머지 변수만 남게된다. 그러므로 계산 그래프에서 역전파는 아래와 같다.
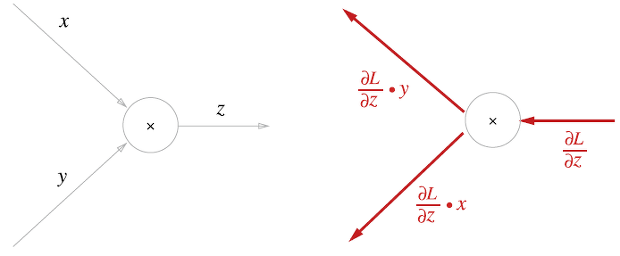
곱셈 노드의 역전파는 상류의 값에 순전파 때의 입력 신호들을 서로 바꿔 곱해 하류로 보낸다. 덧셈의 역전파에서는 상류의 값을 그대로 흘려보내면 되므로 순방향 입력 신호값이 필요하지 않지만, 곱셈의 역전파는 필요하므로 순전파 떄의 값을 저장해놔야 한다.
6. ReLU 노드의 역전파


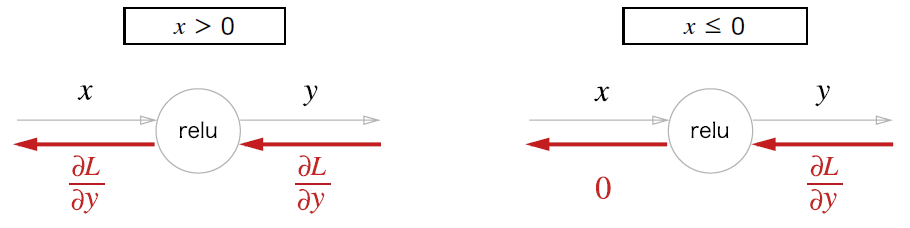
ReLU 노드는 순전파 때의 입력이 0보다 크면 역전파때 상류의 값을 그대로 하류로 흘린다. 그렇지 않은 경우 하류로 신호를 보내지 않는다.
7. Sigmoid 노드의 역전파

시그모이드 함수의 계산 그래프는 위와 같다. $/$노드, 즉 $y={1 \over x}$의 미분은 ${\partial y \over \partial x} = {-{ 1 \over x^{2}}} = -y^{2}$이다. 역전파 때 상류에서 흘러온 값에 $-y^{2}$을 곱해서 하류로 전달한다.
$y=exp(x)$의 미분은 ${\partial y \over \partial x} = exp(x)$이므로 역전파 때 상류에서 흘러온 값에 순전파의 출력을 곱해 하류로 전달한다.
덧셈 노드와 곱셈 노드의 역전파는 이미 알아봤으므로, 이를 토대로 sigmoid 노드의 역전파 값을 구하면 아래와 같다.
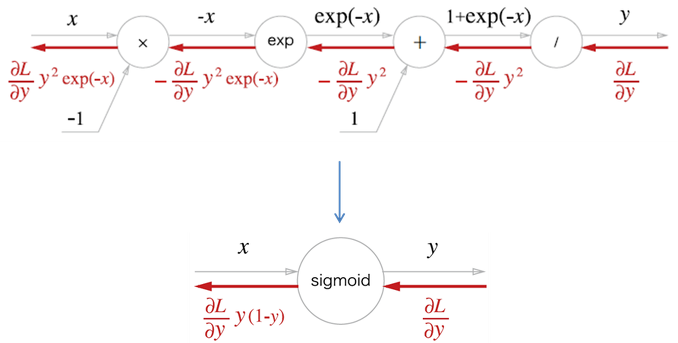
이처럼 sigmoid 노드의 역전파 값은 순전파의 출력 $y$만으로 계산할 수 있다.
8. Affine 노드의 역전파
신경망의 순전파 때 수행하는 행렬의 곱은 기하학에서 어파인 변환이라고 한다.
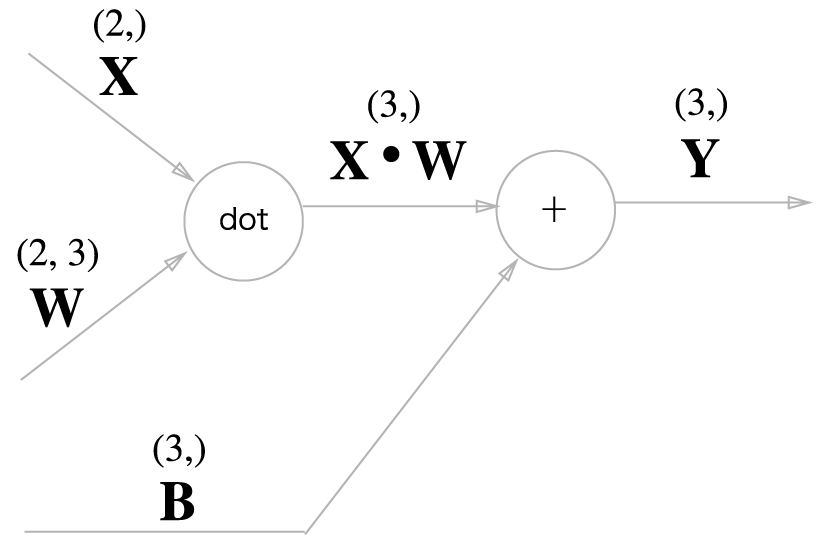
Affine 노드의 계산 그래프는 위와 같다. 하지만 피연산자가 행렬(다차원 배열)이라는 점에 주의해야 한다.
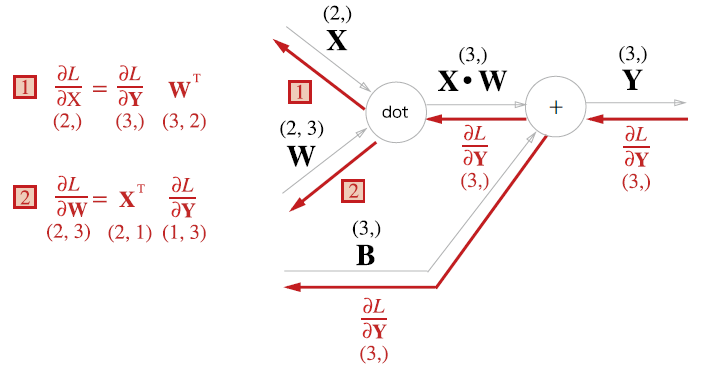
dot 노드의 역전파는 곱셈 노드의 역전파와 비슷하지만, 피연산자가 행렬이라는 점을 고려해야 한다. 기울기 행렬의 크기가 유도되도록 적절히 transpose를 취한다고 생각하면 된다.
예를들어 $\partial L \over \partial X$의 크기는 $(2,$이므로, 역전파 때 상류에서 전달된 값인 $(3,)$ 크기의 $\partial L \over \partial Y$에 $W^{T}$를 내적해야 $(2,)$ 크기의 행렬을 도출할 수 있다.
9. 배치용 Affine 노드의 역전파
학습 때는 데이터를 N개씩 묶어 순전파한다.

주의할 점은 편향에 대한 역전파이다. 순전파 때 같은 편향이 각 데이터에 대한 $X \cdot W$에 더해지므로 역전파 때는 각 데이터의 역전파 값이 모두 하나로 더해져야 한다.
10. Softmax-with-Loss 계층

Softmax 함수는 입력값을 정규화하여 출력한다. 지금부터 Softmax와, 손실 함수인 교차 엔트로피 에러 함수도 포함하여 Softmax-with-Loss 계층으로 설명을 이어갈 것이다.

Softmax-with-Loss 계층의 순전파와 역전파 결과 계산 그래프는 위와 같다. 도출 과정을 살펴볼 필요가 있으므로, Appendix A를 참고하자.
10.1 순전파
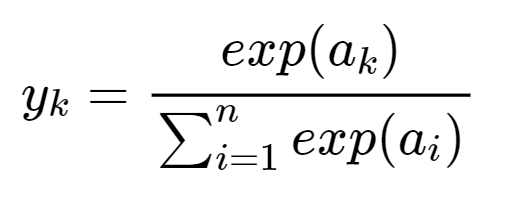
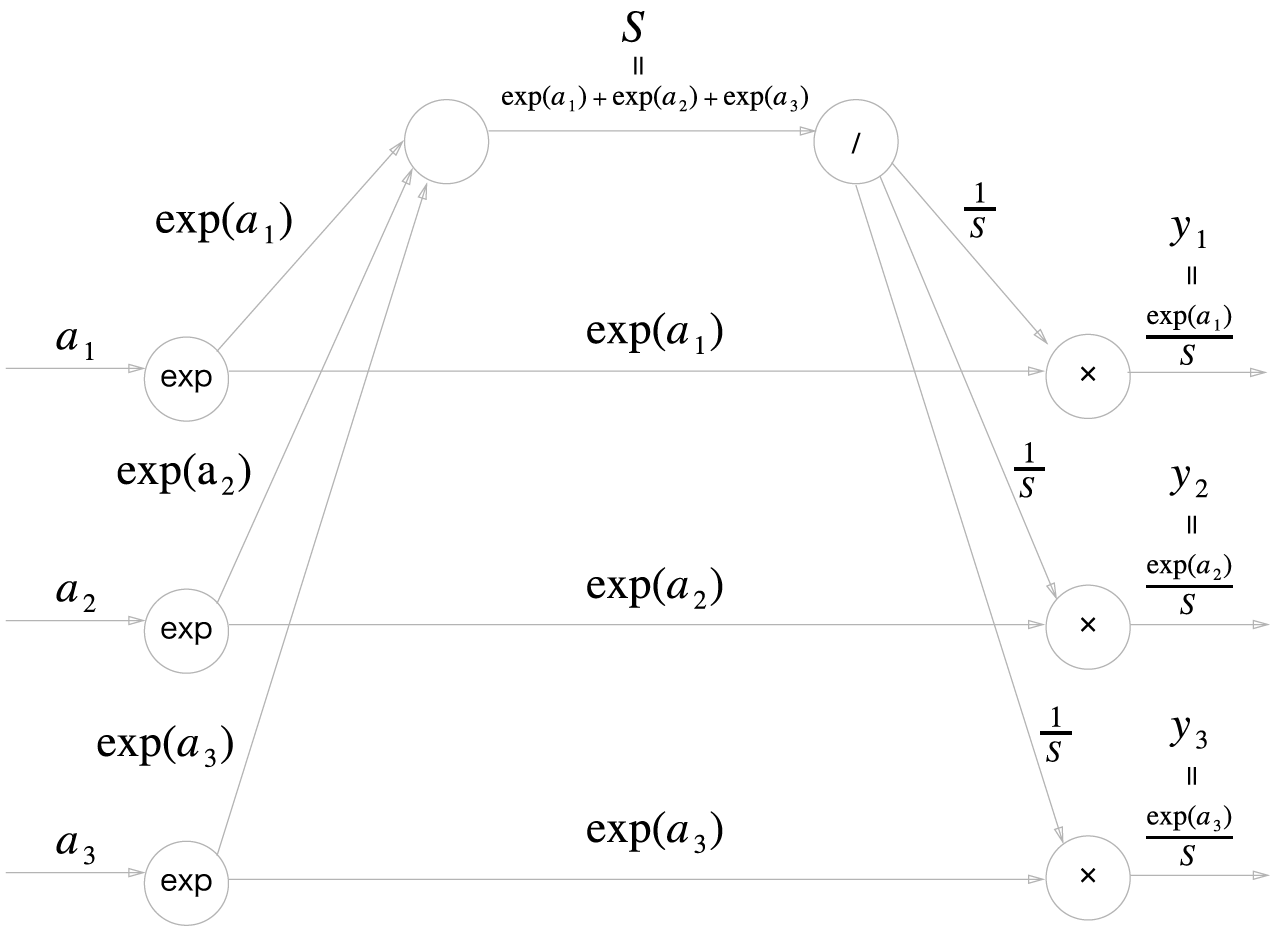
먼저 Softmax 함수의 계산 그래프를 그려 순전파 과정을 보자. 여기서는 $n=3$이라고 가정하자.
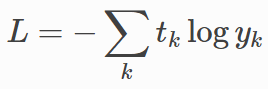
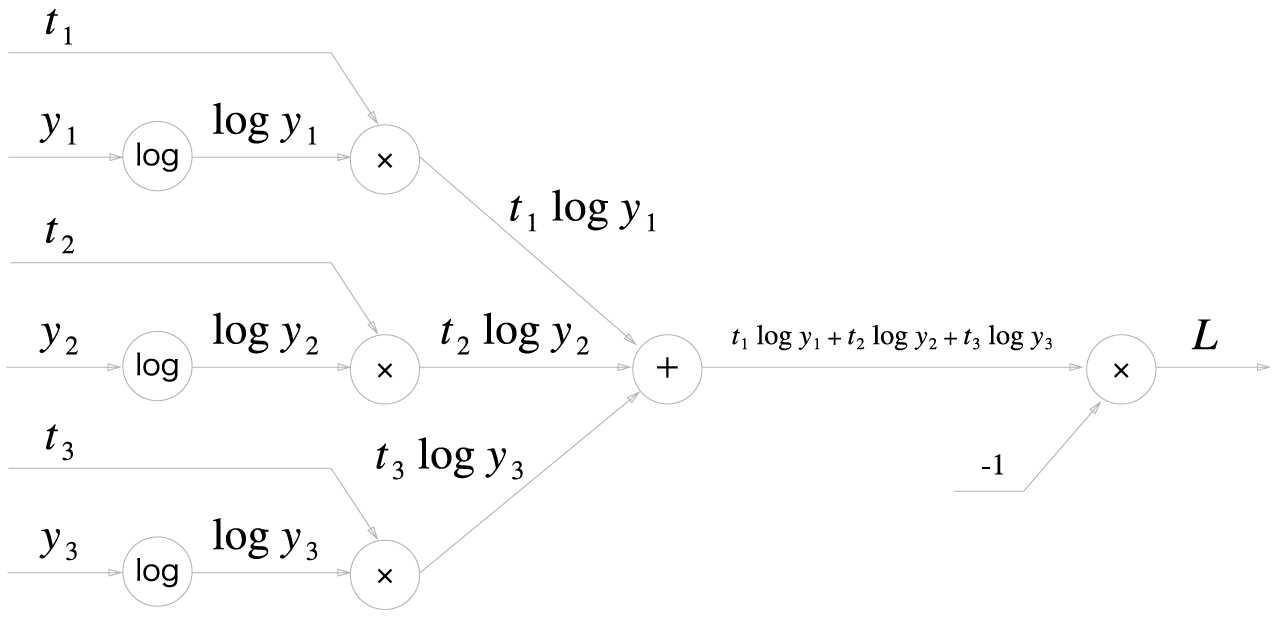
교차 엔트로피 에러 함수의 계산 그래프도 그려서 신경망의 loss가 어떻게 계산되는지 파악해본다.
10.2 역전파

교차 엔트로피 에러 함수를 계산할 때는 자연 로그를 사용하므로, $y=ln x$의 미분은 ${\partial y \over \partial x} = {1 \over x}$이다. 이상의 규칙을 따르면 교차 엔트로피 에러 함수 계층의 역전파는 쉽게 구할 수 있다.

교차 엔트로피 에러 함수 계층에서 계산된 역전파 값이 Softmax 계층으로 흘러온다. 순전파 때 $/$ 노드의 계산값이 여러 노드로 나뉘어 흘렀으므로, 역전파 때는 반대로 흘러온 값들을 더한다. $/$ 노드로 들어오는 각각의 값은 $-{t_{i} \over y_{i}} exp(a_{i})$이며, $y_{i}={exp(a_{i}) \over S}$인 점을 토대로 식을 손보면 $-t_{i} S$이다.
모든 $i$에 대해 값을 더하면 $-S(t_{1}+t_{2}+t_{3})$인데, $/$노드를 거치면서 국소 미분인 $-{1 \over S^{2}}$이 곱해지므로 ${1 \over S} (t_{1} + t_{2} + t_{3})$이 도출된다. 여기서 $t_{i}$는 정답 레이블의 각 원소이므로, 모든 $i$에 대해 $t_{i}$의 합은 $1$이다. 즉 $/$노드의 역전파 값은 $1 \over S$로 깔끔히 떨어진다.
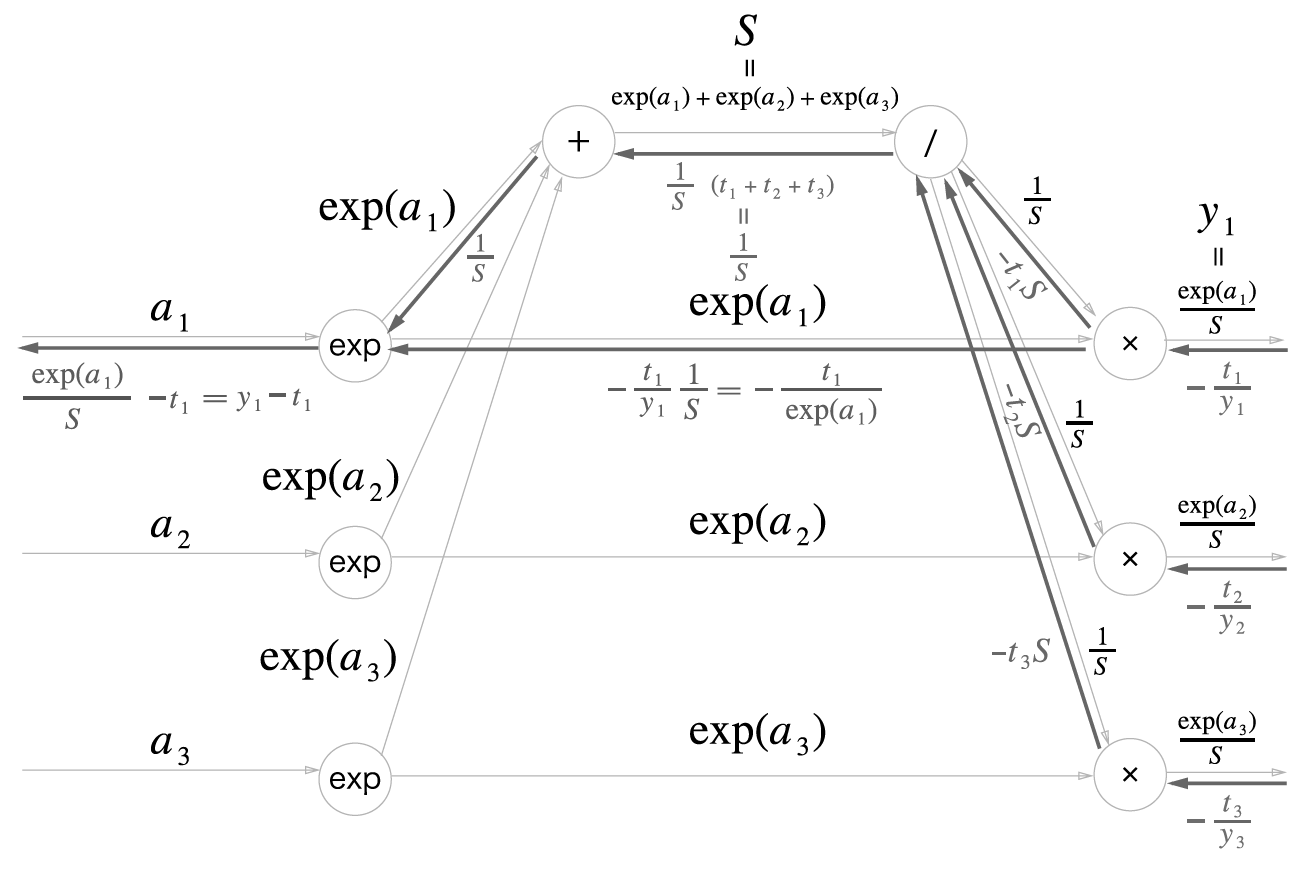
exp 노드의 역전파를 계산하기 전에 $1 \over S$와 $-{t_{i} \over exp(a_{i})}$이 더해진다. 여기에 국소 미분 $exp(a_{i})$가 곱해지는데, 이 값이 곧 $y_{i} - t_{i}$이다.
이는 Softmax 계층의 출력과 정답 레이블의 차분이다. 이런 말끔함은 우연이 아니라, 교차 엔트로피 에러 함수가 애초에 그렇게 설계 되었기 때문이다. 회귀 목적의 신경망 출력층에서 사용하는 항등 함수의 손실 함수로 오차제곱합을 이용하는 이유도 이와 같다. 즉, 항등 함수의 손실 함수로 오차제곱합을 사용하면 역전파의 결과가 $y_{i} - t_{i}$로 말끔히 떨어진다.
softmax-with-loss 계층의 최종 역전파 값은 $(y_{i}-t_{i}) / batch \ size$이다. 교차 엔트로피 에러 함수의 출력값이 배치에 담긴 모든 에러의 합인 것을 고려하면, 역전파 값도 배치의 크기로 나눠줘야 하기 때문이다.
'밑바닥부터 시작하는 딥러닝1' 카테고리의 다른 글
| 가중치 초기화 방법 (0) | 2023.12.09 |
|---|---|
| 매개변수 갱신 방법 (2) | 2023.12.05 |
| 학습 알고리즘 (0) | 2023.11.30 |
| 경사 하강법 (0) | 2023.11.26 |
| 신경망 학습 (0) | 2023.11.26 |
