티스토리 뷰
SVD 역시 PCA와 유사한 행렬 분해 기법을 이용합니다. PCA는 정방행렬만을 고유벡터로 분해할 수 있지만, SVD는 행과 열의 크기가 다른 행렬도 분해할 수 있는 기법입니다. SVD는 $(m\times n)$크기의 행렬 $A$를 $A=U\sum V^{T}$로 분해합니다.
SVD는 특이값 분해로 불리며, 행렬 $U$와 $V$에 속한 벡터는 특이벡터(singular vector)이며, 모든 특이벡터는 서로 직교합니다. $\sum $는 대각행렬이며, 행렬의 대각에 위치한 원소만 0이 아니고 나머지 위치의 값은 모두 0입니다. 대각 원소의 값이 바로 행렬 $A$의 특이값(singular value)입니다. SVD는 $(m\times n)$크기의 행렬 $A$를 $(m\times m)$차원의 $U$, $(m\times n)$차원의 $\sum$, $(n\times n)$차원의 $V^{T}$로 분해합니다.
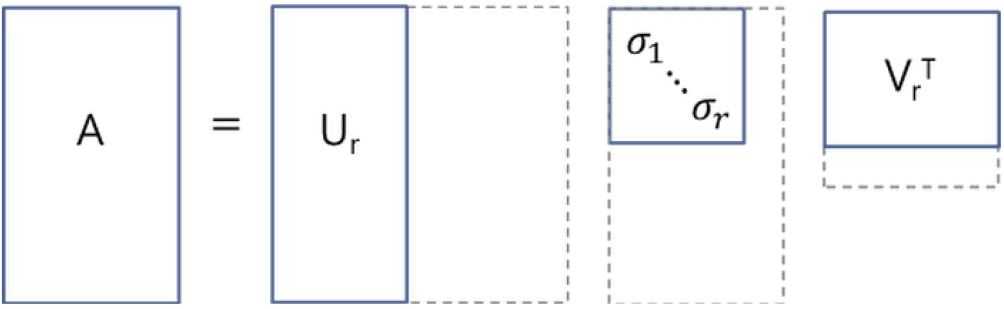
하지만 일반적으로 $\sum$의 특이값이 0인 부분을 모두 제거하고, 제거된 $\sum$에 대응되는 $U$와 $V$ 원소도 함께 제거해 차원을 줄인 형태로 SVD를 적용합니다. 이를 SVD의 compact한 형태로하 하며, 행렬 $A$를 $(m\times p)$차원의 $U$, $(p\times p)$차원의 $\sum$, $(p\times n)$차원의 $V^{T}$로 분해합니다.
Truncaed SVD라는 방법도 있습니다. $\sum$의 대각원소 중에 상위 몇 개만 추출해서 여기에 대응하는 $U$와 $V$의 원소도 함께 제거해 더욱 차원을 줄인 형태로 분해를 수행하는 것입니다. 일반적인 SVD는 보통 넘파이나 사이파이 라이브러리를 이용해 수행합니다. 넘파이를 이용해 SVD 연산을 수행해보겠습니다.

넘파이는 numpy.linalg.svd API로 SVD 연산을 지원합니다. SVD를 적용할 행렬은 랜덤 행렬로 만들었습니다. 랜덤 행렬을 생성하는 이유는 행렬의 개별 로우끼리 의존성을 가지지 않도록 하기 위해서입니다.

랜덤 행렬에 SVD를 적용하여 $U$, $\sum$, $V^{T}$ 행렬을 도출했습니다. numpy.linalg.svd 메서드에 파라미터로 원본 행렬을 입력하면 분해된 세 컴포넌트를 반환합니다. 이때 $\sum$의 경우, 대각 원소에 해당하는 값만 1차원 벡터로 반환합니다(즉, 대각 행렬을 반환하지 않습니다).

분해된 컴포넌트를 다시 행렬곱을 취해서 원본 행렬로 정확히 복원되는지 확인해봅시다. 주의할 점은 $\sum$의 경우 대각 원소만 모든 벡터형태이므로, 행렬곱을 위해 다시 대각행렬로 만들어줘야 한다는 사실입니다. 복원된 행렬은 원본 행렬과 완전히 동일합니다.

이번에는 원본 행렬의 로우 간에 의존성이 있을 경우 $\sum$이 어떻게 변하고, 이에 따른 차원 축소가 진행될 수 있는지 알아봅시다. 로우 간의 의존성을 부여하기 위해 원본 행렬의 세 번째 로우를 첫 번째 로우와 두 번째 로우의 합으로, 네 번째 로우는 첫 번째 로우와 같도록 만들겠습니다.
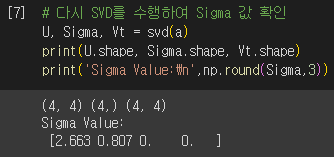
$\sum$ 값중 2개가 0으로 변했습니다. 이는 선형 독립인 로우 벡터의 개수가 2개라는 의미입니다(즉, 행렬의 rank가 2). 특이값이 0인 부분에 대응되는 $U$, $\sum$, $V^{T}$의 부분을 제외하고(compact) 행렬 내적을 수행하더라도 원본 행렬을 그대로 복원할 수 있습니다.
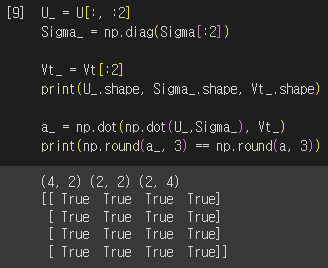
특이값이 0인 부분을 제외하고 행렬곱을 수행하더라고 원본 행렬을 그대로 복원해낸 것을 확인할 수 있습니다.
이번에는 Truncated SVD를 이용해 행렬을 분해해봅시다. Truncated SVD는 $\sum$ 행렬의 특이값 중 상위 일부 데이터만 추출해 분해하는 방식입니다. 이렇게 분해하면 인위적으로 더 작은 차원의 $U$, $\sum$, $V^{T}$로 분해하기 때문에 원본 행렬을 정확히 복원할 수는 없습니다. 하지만 상당한 수준으로 원본 행렬을 근사할 수 있습니다. 당연한 얘기지만, 더 많이 잘라낼수록(truncate) 원본 행렬에 대한 복원 정확도가 떨어집니다.
Tuncated SVD는 넘파이가 아닌 사이파이에서만 지원됩니다. Truncated SVD는 희소 행렬로만 지원돼서 spicy.sparse.linalg.svds를 이용해야 합니다.

랜덤하게 생성된 $(6\times 6)$ 크기의 원본 행렬을 Normal SVD로 분해한 뒤, 분해된 행렬의 차원과 특이값을 확인합시다. 또한 원본 행렬을 truncated SVD로 분해한 뒤, 분해된 행렬의 차원과 특이값, 다시 내적했을 때 원본 행렬을 얼마나 잘 근사하는 지를 확인합시다. spicy.sparse.linalg.svds 메서드의 파라미터로 몇 개의 특이값을 truncate할 지를 설정할 수 있습니다. 여기선 2개의 특이값을 잘라내기 위해, 남은 특이값의 개수인 4로 설정해줘야 합니다.
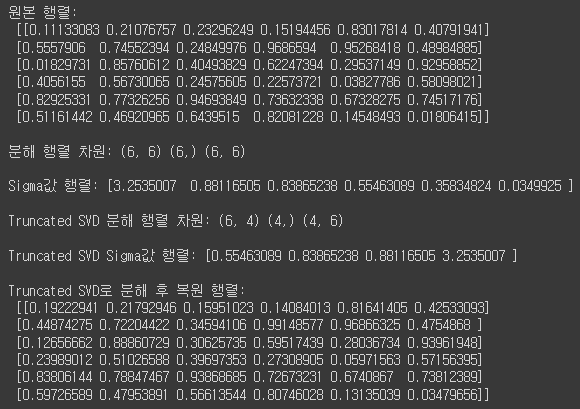
Truncated SVD로 분해된 행렬로 다시 복원을 시도할 경우, 원본 행렬로 완벽히 복원되진 않고 근사적으로 복원됨을 알 수 있습니다.
사이킷런의 TruncatedSVD 클래스를 이용하여 Truncated SVD를 수행할 수도 있습니다. 하지만 해당 클래스는 원본 행렬을 분해한 $U$, $\sum$, $V^{T}$ 행렬을 반환하지는 않습니다. 사이킷런의 PCA 클래스와 유사하게 fit()과 transform() 메서드를 호출해 원본 데이터를 몇 개의 주요 피처(Trunckated SVD의 k 값)로 차원을 축소해 변환합니다. 원본 데이터를 $U\sum$ 행렬에 선형 변환하여 변환을 하는 것입니다.

붓꽃 품종 분류 데이터 세트를 Truncated SVD를 이용하여 차원 축소 시켜봅시다.

Truncated SVD를 통해 4개의 피처를 2개의 피처로 압축하더라도 세 종류의 붓꽃이 꽤 잘 구분되는 것을 확인할 수 있습니다.

사이킷런의 TruncatedSVD와 PCA 클래스는 모두 SVD를 이용해 행렬을 분해합니다. 붓꽃 데이터의 레이블을 제외한 피처에 표준화 스케일링을 적용한 뒤 TruncatedSVD와 PCA 변환을 적용한 결과를 확인해봅시다.


각 품종이 클러스터 된 모양을 시각화해보았는데, 그냥 같아보입니다. 두 변환을 통해 압축된 피처 데이터의 값을 비교해보아도 차이의 평균이 거의 0에 가깝습니다. 이는 두 변환이 서로 동일한 동작을 수행함을 의미합니다. 즉, 스케일링으로 데이터 중심이 동일해지면 사이킷런의 Truncated SVD와 PCA는 동일한 변환을 수행합니다. 이는 PCA가 SVD로 구현됐음을 의미합니다. 하지만 PCA는 밀집 행렬(dense matrix)에 대한 변환만 가능하며, SVD는 희소 행렬(sparse matrix)에 대한 변환도 가능합니다.
SVD는 PCA와 유사하게 컴퓨터 비전 영역에서 이미지 압축을 통한 패턴 인식과 신호 처리 분야에 사용됩니다. 또한 텍스트 토픽 모델링 기법인 LSA(Latent Semantic Analysis)의 기반 알고리즘입니다.
'파이썬 머신러닝 완벽 가이드' 카테고리의 다른 글
| 파이썬 머신러닝 완벽 가이드 : K-means clustering (0) | 2023.05.23 |
|---|---|
| 파이썬 머신러닝 완벽 가이드 : NMF(Non-Negative Matrix Factorization) (0) | 2023.05.23 |
| 파이썬 머신러닝 완벽 가이드 : LDA(Linear Discriminant Analysis) (0) | 2023.05.22 |
| 파이썬 머신러닝 완벽 가이드 : PCA 실습 - UCI 신용카드 고객 데이터 세트 (0) | 2023.05.22 |
| 파이썬 머신러닝 완벽 가이드 : 차원 축소 개요와 PCA(Principal Component Analysis) (0) | 2023.05.22 |
