티스토리 뷰
지금까지 머신러닝 모델의 하이퍼 파라미터 튜닝을 위해 사이킷런의 GridSearch() 메서드를 이용했습니다. 해당 메서드의 주요 단점은, 튜닝할 파라미터의 개수가 많아지거나 값의 범위가 넓을수록 최적화 수행 시간이 기하급수적으로 길어진다는 점입니다.
그라디언트 기반 앙상블 알고리즘은 성능이 매우 뛰어나지만, 하이퍼 파라미터의 개수가 많으므로 GridSearch() 메서드를 이용한 튜닝이 현실적으로 어려울 수 있습니다. 때문에 실무 및 Competition과 같은 상황에선 GridSearch 방식보다는 베이지안 최적화 기법을 이용해 하이퍼 파라미터 튜닝을 하곤 합니다.
베이지안 최적화는 블랙박스 형태의 목적 함수의 최대 또는 최소 값을 도출하는 입력값을 가능한 적은 시도를 통해 빠르고 효과적으로 찾아줍니다. 베이지안 확률이 새로운 사건의 관측이나 샘플 데이터를 기반으로 사후 확률을 개선하듯이, 베이지안 최적화는 새로운 데이터를 통해 최적 함수를 예측하는 사후 모델을 개선합니다.
베이지안 최적화는 대체 모델(Surrogate Model)과 획득 함수(Acquisition Function)의 요소로 구성됩니다. 대체 모델은 획득 함수로부터 최대/최소 값을 도출하는 입력값을 추천받은 뒤, 이를 기반으로 실제 함숫값을 관측하여 최적 함수 모델을 개선합니다. 획득 함수는 개선된 대체 모델을 기반으로 최적 입력값을 다시 예측하여 추천합니다. 베이지안 최적화로 하이퍼 파라미터 튜닝을 할 시, 입력값은 하이퍼 파라미터이며 찾고나 하는 최대/최소값은 모델의 성능 지표값입니다.
베이지안 최적화 과정을 차례차례 알아봅시다.

최초에, 랜덤한 하이퍼 파라미터를 기반으로 모델을 학습시킨 뒤 성능 지표를 관측합니다. 주황색 사선이 찾아야 할 실제 최적함수이며, 검은색 데이터가 관측값입니다.

관측값을 기반으로 대체 모델은 최적 함수를 추정합니다. 파란색 실선이 대체 모델이 추정한 최적 함수이며, 음영 영역은 예측 함수의 신뢰 구간입니다. 즉, 일종의 불확실성입니다. 이때 관측값 중 최댓값을 기록한 하이퍼 파라미터를 최적 관측값이라고 합시다.

추정된 최적함수를 기반으로 획득 함수는 최댓값을 가질 가능성이 가장 높은 하이퍼 파라미터를 예측하여 대체 모델에게 다시 전달합니다.

획득 함수가 추천한 하이퍼 파라미터에 해당하는 관측값을 기반으로 최적 함수를 다시 추정합니다.
이러한 알고리즘을 특정 횟수만큼 반복하게 되면 대체 모델의 불확실성이 개선되고 점차 정확한 최적 함수 추정이 가능합니다. 대체 모델이 최적 함수를 추정할 때 보통 가우시안 프로세스 알고리즘을 사용합니다. 하지만 실습에서 사용할 HyperOpt 라이브러리는 트리 파르젠(TPE) 알고리즘을 사용합니다.
베이지안 최적화를 머신러닝 모델의 하이퍼 파라미터 튜닝에 사용할 수 있게 도와주는 여러 파이썬 패키지가 있습니다. 대표적으로 HyperOpt, Bayesian Optimization, Optuna 등이 있으며 사용법은 크게 다르지 않습니다. 책에선 HyperOpt 라이브러리를 사용합니다.
HyperOpt를 사용하는 주요 로직입니다.
- 입력 변수명과 입력값의 검색 공간을 설정
- 목적 함수를 설정
- 목적 함수의 최솟값을 가지는 입력값을 유추
주의할 점은, 다른 패키지와는 다르게 목적함수의 최댓값이 아닌, 최솟값을 반환하는 입력값을 찾는다는 것입니다.

HyperOpt의 hp 모듈을 이용하여 입력 변수명과 입력값의 검색 공간을 설정합니다. 변수명과 검색 공간은 딕셔너리 형태여야 합니다. hp 모듈은 다양한 검색 공간을 설정할 수 있도록 여러 메서드를 제공합니다. 가령, quniform() 메서드로 -10부터 10까지의 값을 1의 간격으로 구성했습니다.
- hp.quniform(label, low, high, q) : low ~ high까지 q의 간격으로 검색 공간 설정
- hp.uniform(label, low, high) : low ~ high까지 정규 분포 형태의 검색 공간 설정
- hp.randint(label, upper) : 0 ~ upper까지 랜덤한 정숫값으로 검색 공간 설정
- hp.loguniform(), hp.choice() 등의 다른 메서드가 존재

목적 함수를 정의했습니다. 목적 함수는 반드시 입력값과 검색 공간을 설정한 딕셔너리를 인자로 받고, 특정 값을 반환해야 합니다. 반환값은 딕셔너리 형태가 될 수도 있으나, {'loss' : retval, 'status' : STATUS_OK}과 같이 loss와 status를 키로 설정해야 합니다.

본격적인 베이지안 최적화를 수행하는 fmin(objective, space, algo, max_evals, trials) 메서드입니다. 각 함수의 파라미터는 아래와 같습니다.
- fn : 목적 함수
- space : 입력값과 검색 공간이 담긴 딕셔너리
- algo : 베이지안 최적화 전용 알고리즘. 기본적으로 tpe.suggest(TPE).
- max_evals : 최적 입력값을 찾기 위한 시도 횟수
- trials : 시도한 입력값과, 그에 따른 목적 함수의 반환값을 저장하는 Trials 객체.
- rstate : 베이지안 최적화를 위한 랜덤 시드. 고정값 설정시 매번 같은 결과.
fmin() 메서드의 반환값은 찾은 최적 입력값입니다. x=-4.0, y=12.0가 도출됐습니다. 물론 시도 횟수를 늘릴수록 더욱 최적화된 입력값을 얻을 수 있습니다.


fmin() 메서드의 인자로 들어가는 Trials 객체는 시도한 입력값에 따른 함숫갑을 속성으로 기록합니다. 중요 속성으로 results와 vals가 있습니다. result는 반환값이며, vals는 시도한 입력값입니다.

판다스의 DataFrame 객체로 입력값에 따른 함수 반환값을 보기 쉬운 형태로 요약할 수 있습니다.
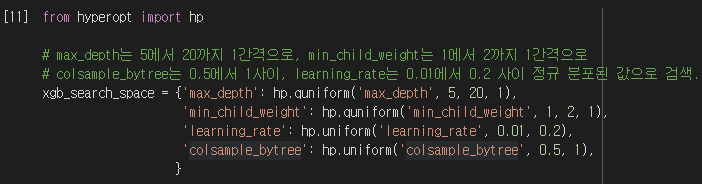
HyperOpt를 이용하여 XGBoost의 하이퍼 파라미터를 최적화 해보겠습니다. 먼저 튜닝할 하이퍼 파라미터와, 검색 공간을 정의합니다.

목적함수를 정의합니다. 주의해야 할 점은, HyperOpt는 입력값과 반환값이 모두 실수형 자료형이므로, XGBoost의 하이퍼 파라미터 설정시 정수형 타입으로 입력해야 하는 인자에 대해서는 형변환을 해줘야 한다는 것입니다. 또한 목적 함수의 최솟값을 찾게 되므로, 교차 검증의 평균 정확도에 -1을 곱한 값을 반환해야 합니다.
주의해야 할 점은, cross_val_score() 메서드를 XGBoost나 LightGBM 모델에 적용할 경우 조기 중단 기능을 사용할 수 없다는 것입니다. 조기 중단을 위해선 KFold로 학습과 검증용 데이터 세트를 만들어서 직접 교차 검증을 수행해야 합니다.


베이지안 최적화를 통해 찾아낸 하이퍼 파라미터입니다.

fmin()으로 추출된 최적 하이퍼 파라미터를 XGBClassifier 객체에 인자로 전달하기 전에, 마찬가지로 정수형 하이퍼 파라미터를 위한 형변환을 해줘야 합니다.

최적 하이퍼 파라미터로 학습시킨 XGBClassifier 모델의 예측 성능을 테스트 데이터로 평가한 결과입니다. 워낙 작은 데이터 세트로 학습, 검증, 테스트를 수행했기 때문에 fmin() 메서드 인자의 rstate 값을 변경할 경우 불안정한 성능 결과가 도출될 수 있습니다.
'파이썬 머신러닝 완벽 가이드' 카테고리의 다른 글
| 파이썬 머신러닝 완벽 가이드 : 캐글 신용카드 사기 검출 분류해보기 (0) | 2023.05.06 |
|---|---|
| 파이썬 머신러닝 완벽 가이드 : XGBoost, LightGBM으로 캐글 산탄데르 고객 만족 예측해보기 (0) | 2023.05.05 |
| 파이썬 머신러닝 완벽 가이드 : LightGBM (0) | 2023.05.03 |
| 파이썬 머신러닝 완벽 가이드 : XGBoost(eXtra Gradient Boost) (0) | 2023.05.03 |
| 파이썬 머신러닝 완벽 가이드 : 그라디언트 부스팅 머신(GBM) (0) | 2023.05.02 |
