Strongly Connected Component (SCC)

'강한연결요소'라고 불리는 Strongly Connected Component (SCC)에 대해 알아봅시다.

 

1. SCC의 정의

방향 그래프 $G=(V, E)$에서, 어느 노드들의 그룹 $X$가 있다고 했을 때, $X$에서 임의의 두 노드 $u, v$를 골랐을 때 $u$에서 $v$로 가는 경로가 존재한다라는 조건을 만족시키면 $X$를 strongly connected component라고 합니다. SCC의 정의는 maximal하게 형성된 strongly connected component입니다. maximal하다는 것이 무엇인지 아래의 예시를 통해 알아봅시다.

 

 

위와 같은 방향 그래프에서 세 노드로 구성된 초록색 그룹이 SCC입니다. 파란색 노드는 그 자체로서 SCC입니다. 그런데 두 개의 초록색 노드를 골라 stronly connected component를 만들 수 있습니다. 하지만 해당 그룹이 SCC인 것을 아닙니다. 왜냐하면 모든 초록색 노드로 구성한 그룹이 더 큰(maximal) stronly connected component 이기때문입니다.

 

이러한 maximal한 속성 때문에, 서로 다른 두 SCC에서 임의로 각각 노드 한 개를 뽑아서 $u, v$라고 한다면, $u$에서 $v$로 가는 경로가 존재하면서 $v$에서 $u$로 가는 경로도 존재하는 경우는 없습니다. 이렇듯 SCC 간의 관계가 acyclic할 수 밖에 없는 이유는, 만약 서로 다른 SCC 간에 사이클이 존재한다면 그러한 SCC를 모두 합친 그룹이 더 큰 SCC이기 때문입니다.

 

 

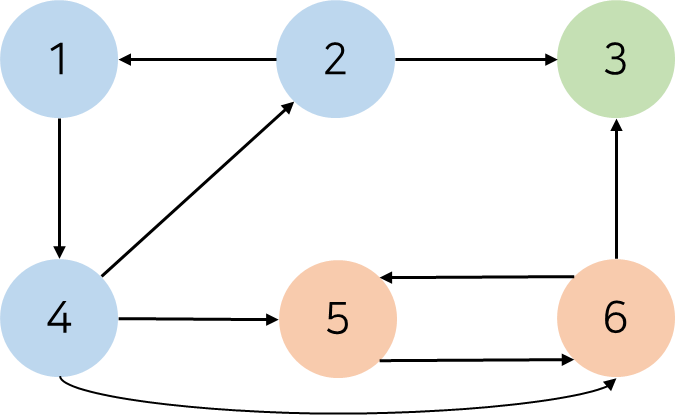
예를들어 위와 같은 방향 그래프가 있고, 서로다른 SCC끼리 색으로 구분해놓은 상태입니다. 이러한 방향 그래프에서 SCC를 하나의 supernode로 취급하면 아래와 같은 DAG를 얻을 수 있다는 것 또한 매우 중요한 사실입니다.

 

 

 

2. SCC를 찾는 알고리즘

방향 그래프에서 SCC를 찾는 알고리즘은 크게 두 가지가 있습니다. Kosaraju's Algorithm과 Tarjan's Algorithm입니다. 두 알고리즘 모두 깊이우선탐색(dfs)을 이용합니다. 또한, Tarjan's Algorithm는 전자에 비해 조금 이해하기 어렵지만 PS 등의 분야에서 SCC를 응용함에 있어 확장성이 높다고 알려져 있습니다.

 

 

2.1. Kosaraju's Algorithm

DAG에선 깊이우선탐색을 이용하여 위상 정렬을 할 수 있습니다. dfs 중 탐색이 늦게 완료된 순서대로 노드를 정렬하면 위상정렬을 할 수 있다는 사실은 잘 알려져있습니다. 이때, "노드 $u$의 탐색이 완료되었다"라는 말은, 깊이우선탐색 도중 노드 $u$의 모든 자식이 탐색 완료된 시점을 의미합니다. 깊이우선탐색 도중 노드의 방문 순서와 노드의 탐색 순서는 dfs tree에 잘 드러나 있습니다.

 

 

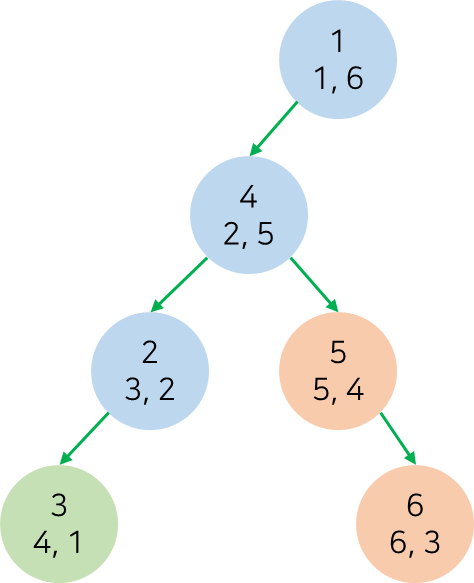
노드$1$부터 dfs를 수행했을 때의 dfs tree이며, 각 노드의 아래에는 (방문 순서, 탐색 순서)가 기록되어 있습니다. 또한, 탐색 순서가 빠른 노드부터 마킹하는 것을 post order라고 합니다.

 

 

원래의 방향 그래프에서 각 노드에 post order를 표시하면 다음과 같은데, 이때 우리는 각 SCC에 포함되는 모든 노드 중 maximum post order(밑줄 친 값) 값은 SCC 간의 위상정렬 순서를 간직하고 있는 것을 확인할 수 있습니다.

 

이때, 원래의 방향 그래프 $G$의 모든 간선의 방향을 뒤집은 그래프를 $G^{'}$라고 합시다. 그리고 $G$에서 dfs를 수행함으로써 얻은 각 노드의 post order를 $p[i]$라고 합시다. Kosaraju's Algorithm은 $G^{'}$에서 $p[i]$가 큰 노드 순서대로 dfs를 수행했을 때, dfs tree에 묶이는 노드의 집합이 $G$에서 하나의 SCC라는 사실을 이용합니다.

 

 

 

$G^{'}$에서 post order가 큰 노드 순서대로 dfs를 수행하면, 그 노드가 속하는 SCC에 포함된 노드들만 dfs tree에 엮인다는 것인데 이를 어떻게 증명할까요? 일단 그 노드가 속하는 SCC에 포함되는 다른 모든 노드를 방문함은 자명합니다. $G$와 $G^{'}$의 SCC는 같기 때문입니다. SCC에 속하지 않는 노드가 dfs tree에 엮이지 않는 이유는, 그러한 노드로 이동하는 간선이 존재한다고 해도 이미 해당 노드는 이미 다른 dfs tree에 엮여있기 때문입니다.

 

우리는 $G^{'}$에서 노드$1$부터 dfs를 수행할 것입니다. 그러면 노드$1, 2, 4$가 같은 dfs tree에 엮이고 dfs가 종료됩니다. 그 다음은 노드$5$에서 dfs를 수행할 차례입니다. 여기서 시작된 dfs는 노드$4$를 방문할 수 있지만, 이미 노드$4$는 노드$1$에서 시작한 dfs tree에 포함되어 있으므로 방문이 불가능합니다. 그러므로 노드$5$에서 시작된 dfs tree에 엮이지 않습니다.

 

Kosaraju's Algorithm은 $G, G^{'}$에서 각각 dfs를 수행하므로, $O(|V|+|E|)$의 시간복잡도를 가집니다. 또한, $G$에서 post order가 큰 순서대로 노드를 정렬하는 것은 dfs 중 stack에 노드를 삽입함으로써 쉽게 구현할 수 있습니다.

 

 

BOJ 2150 : Strongly Connected Component

#include <bits/stdc++.h>
#define sz(x) (int)x.size()
#define all(x) x.begin(), x.end()
using namespace std;
vector<int> adj[10001], radj[10001];
int vis[10001];
stack<int> st;
vector<vector<int>> scc;

void go(int n) {
	vis[n] = 1;
	for (int a : adj[n]) {
		if (vis[a]) continue;
		go(a);
	}
	st.push(n);
}

void find(int n, int idx) {
	vis[n] = 1;
	scc[idx].push_back(n);
	for (int a : radj[n]) {
		if (vis[a]) continue;
		find(a, idx);
	}
}

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);

	int N, M;
	cin >> N >> M;

	// construct G, G'
	for (int i = 1; i <= M; i++) {
		int a, b;
		cin >> a >> b;
		adj[a].push_back(b);
		radj[b].push_back(a);
	}

	// dfs for post ordering
	for (int i = 1; i <= N; i++) {
		if (vis[i]) continue;
		go(i);
	}

	memset(vis, 0, sizeof(vis));

	// dfs to find SCCs in G
	int idx = -1;
	while (!st.empty()) {
		int cur = st.top();
		st.pop();
		if (vis[cur]) continue;
		scc.push_back(vector<int>());
		find(cur, ++idx);
	}

	for (int i = 0; i < sz(scc); i++) {
		sort(all(scc[i]));
	}
	sort(all(scc));

	cout << sz(scc) << "\n";
	for (int i = 0; i < sz(scc); i++) {
		for (int j = 0; j < sz(scc[i]); j++) {
			cout << scc[i][j] << " ";
		}
		cout << -1 << "\n";
	}
}

 

 

 

2.2. Tarjan's Algorithm

Kosaraju's Algorithm이 두 번의 dfs를 통해 SCC를 찾아냈다면, Tarjan's Algorithm은 한 번의 dfs만으로 SCC를 찾아냅니다. 그러므로 $G$의 모든 간선의 방향을 뒤집은 $G^{'}$도 필요하지 않습니다. 하지만 일반적으로 Kosaraju's Algorithm보다 동작 원리를 이해하기 어렵습니다.

 

우리는 먼저 방향 그래프에서의 간선 분류에 대해 알아야 합니다.

 

1) Tree edge

방향 그래프의 간선$(u → v)$ 중, dfs tree에 존재하는 간선을 의미합니다.

 

2) Back edge

방향 그래프의 간선$(u → v)$ 중, dfs tree 상에서 $v$가 $u$의 조상인 간선입니다.

그러므로 dfs tree 상에서 이 간선을 표시하면 자신의 조상으로 올라가는 간선이 됩니다.

 

3) Forward edge

방향 그래프의 간선$(u → v)$ 중, dfs tree 상에서 $u$가 $v$의 조상인 간선입니다.

즉, dfs tree 상에서 이 간선을 표시하면 자신의 자손으로 내려가는 간선이 됩니다.

 

4) Cross edge

방향 그래프의 간선$(u → v)$ 중, 위의 세 가지 종류에 해당하지 않는 나머지 간선입니다.

 

 

우리의 방향 그래프 $G$에서 간선 분류를 수행하면 아래와 같습니다.

 

 

이를 dfs tree 상에서 표현하면 아래와 같습니다.

 

 

또한, dfs 도중 각 노드의 방문 순서를 노드 아래에 기록했습니다. 이 값을 $vis[u]$라고 합시다. 추가로, Tarjan's Algorithm을 수행하려면 각 노드 별로 아래의 값을 알아야합니다.

 

$l[u] : $ dfs tree 상에서 노드 $u$를 루트로 하는 sub-tree에서, 하나의 간선을 거쳐 갈 수 있는 제일 작은 $vis$ 값(사실 이 정의는 틀렸습니다. 그 이유는 아래 설명을 통해 알 수 있습니다).

 

dfs 도중 노드 $u$에 방문했을 시, $l[u] = vis[u]$로 일단 초기화 됩니다. 그 후 sub-tree에 있는 노드들을 반영되어 $l[u]$가 업데이트 됩니다. 최종적으로 $l[u]$ 값이 정해졌을 때, $l[u] = vis[u]$라면 $u$를 루트로 하는 sub-tree가 하나의 SCC가 됩니다. 즉, $u$의 모든 자손들은 $u$를 거치지 않고서는 $u$보다 위에 있는 노드에 도달할 수 없다는 뜻입니다.

 

만약 $l[u] < vis[u]$라면, 즉 $u$보다 더 높이 있는 노드에 도달할 수 있다면 $u$를 루트로 하는 sub-tree는 SCC가 될 수 없습니다. 왜냐하면 $u$를 루트로 하는 sub-tree는 더 큰 SCC에 속하는 것이기 때문입니다. 또한, $l[u] =  vis[u]$로 초기화 했으므로 $l[u] > vis[u]$인 경우는 없습니다.

 

dfs 도중 $l[u]$를 업데이트하는 구체적인 방법을 설명하겠습니다. 일단 $u$와 인접한 다른 노드를 $v$라고 하겠습니다. 만약 $v$가 아직 방문하지 않는 노드라면, 이제 $u$에서 $v$로 dfs가 호출되므로 $(u → v)$는 tree edge가 됩니다. 그리고 $l[u] = \min (l[u], l[v])$로 업데이트합니다.

 

$v$가 방문된 노드라면 두 가지 경우로 나뉘는데, 이미 다른 SCC에 포함이 되었다고 결정된 노드$(u → v : Cross edge)$와, 그렇지 않는 노드$(u → v : Back edge)$입니다. Back edge의 경우 $v$는 $u$보다 더 위에 있으므로 $l[u]= \min (l[u], vis[v])$로 업데이트 합니다.

 

즉, cross edge인 경우에는 $v$가 아직 어떤 SCC에 포함된다고 결정이 되지 않은 경우만 $l[u] = \min (l[u], vis[v])$로 업데이트 해야합니다. 이와 같이, $l[u]$를 업데이트함에 있어서 걸러야 되는 간선이 존재하기 때문에 위의 $l[u]$의 정의는 틀렸습니다. 하지만 이러한 예외를 정의에 녹아들게 하려면 정의가 복잡해지므로 그냥 두었습니다.

 

 

 

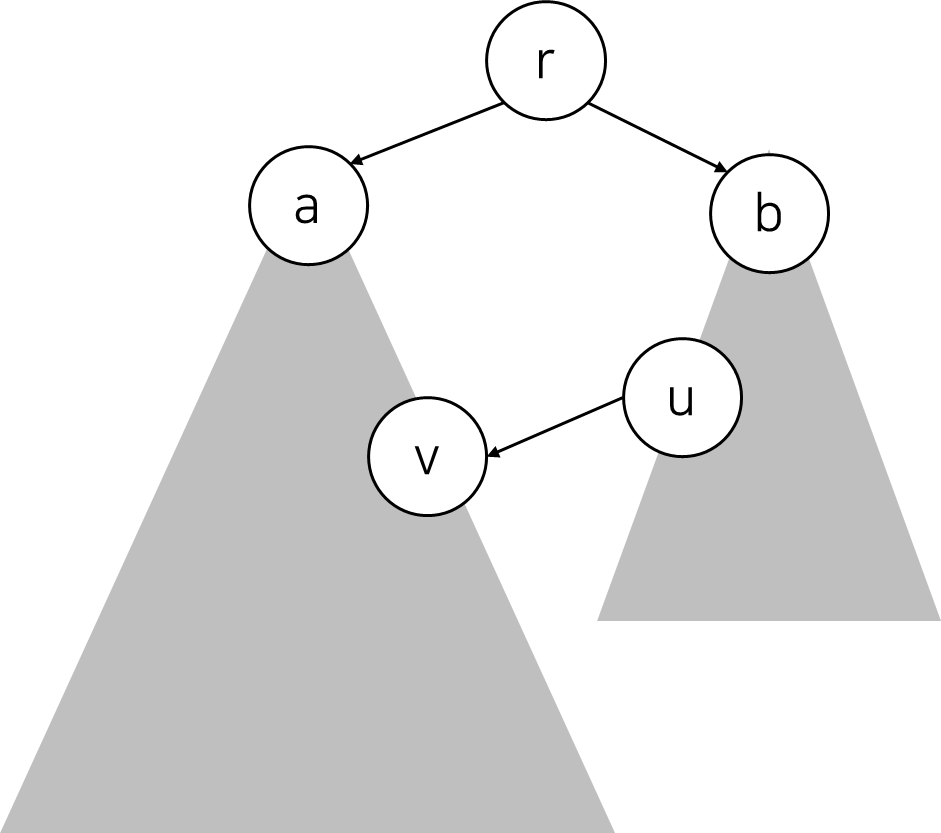
이미 다른 SCC에 포함된다고 결정된 $v$로 이동하는 간선에 대해선 업데이트를 수행하면 안 되는 이유를 설명하겠습니다. 위 그림과 같이, 만약 $u$에서 $v$로 가는 cross edge가 있고, $v$는 아직 SCC에 포함되지 않은 상태라고 가정합시다. 그렇다면 $v$는 노드 $a$보다 더 위에 있는 노드로 이동할 수 있다는 뜻이 됩니다. 즉 노드 $r$에 도달 가능하며, 결국 $u$까지 올 수 있습니다. 그러므로 $r$을 루트로 하는 sub-tree는 하나의 SCC안에 포함될 수 있다는 뜻입니다.

 

그런데 이미 $a$를 루트로 하는 sub-tree가 하나의 SCC로 결정되었다고 합시다. 그렇다면 $v$는 $a$보다 위에 있는 노드에 도달할 수 없기 때문에 $u$에 도달할 수 없습니다. 즉, $u$와 $v$는 같은 SCC에 존재할 수 없기 때문에 업데이트를 하지 않는 것입니다.

 

 

BOJ 2150 : Strongly Connected Component

#include <bits/stdc++.h>
#define sz(x) (int)x.size()
#define all(x) x.begin(), x.end()
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<ll, int> pli;
vector<int> adj[10001];
int vis[10001], low[10001], scc[10001], cnt;
stack<int> st;
vector<vector<int>> ans;

void go(int n) {
	vis[n] = ++cnt;
	st.push(n);
	low[n] = vis[n];

	for (int a : adj[n]) {
		// tree edge
		if (!vis[a]) {
			go(a);
			low[n] = min(low[n], low[a]);
		}
		// backward edge and cross edge that scc[a] == 0
		else if(!scc[a]){
			low[n] = min(low[n], vis[a]);
		}
	}

	if (low[n] == vis[n]) {
		vector<int> vec;
		while (!st.empty()) {
			int cur = st.top();
			st.pop();
			scc[cur] = 1;
			vec.push_back(cur);
			if (cur == n) break;
		}
		sort(all(vec));
		ans.push_back(vec);
	}
}

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);

	int N, M;
	cin >> N >> M;

	for (int i = 1; i <= M; i++) {
		int a, b;
		cin >> a >> b;
		adj[a].push_back(b);
	}

	for (int i = 1; i <= N; i++) {
		if (!vis[i]) go(i);
	}

	cout << sz(ans) << '\n';
	sort(all(ans));
	for (auto vec : ans) {
		for (auto k : vec) cout << k << " ";
		cout << "-1\n";
	}
}