티스토리 뷰
지금까지 설명한 회귀는 독립변수와 종속변수의 관계가 일차 방정식 형태로 표현된 회귀였습니다. 회귀가 독립변수의 단항식이 아닌, 2차 3차 방정식과 같은 다항식으로 표현되는 것을 다항(Polynomial) 회귀라고 합니다. 즉, 다항 회귀는 $Y = W_{0} + W_{1}X_{1} + W_{2}X_{1}X_{2} + W_{3}X_{3}^{2}$와 같이 표현됩니다.
주의할 점은, 다항 회귀를 비선형 회귀로 혼동할 수 있다는 점입니다. 다항 회귀는 선형 회귀라는 점을 기억해야 합니다. 회귀에서 선형/비선형을 나누는 기준은 회귀 계수의 선형/비선형성이기 때문입니다. 독립 변수의 선형/비선형 여부와는 무관합니다.

위의 그림과 같이, 독립 변수와 종속 변수의 관계를 단순 선형 회귀로 모델링하는 것 보다 다항 회귀로 모델링했을 때 예측 성능이 더 높은 경우가 존재합니다.
아쉽지만 사이킷런은 다항 회귀를 위한 클래스를 명시적으로 제공하지 않습니다. 하지만 다항 회귀 역시 선형 회귀이므로 비선형 함수를 선형 모델에 적용시키는 방법을 사용해 구현합니다. 사이킷런은 PolynomialFeatures 클래스를 통해 피처를 Polynomial(다항식) 피처로 변환합니다. degree 인자를 통해 입력받은 단항식 피처를 degree에 해당하는 다항식 피처로 변환합니다. 다른 전처리 변환 클래스와 마찬가지로, fit(), transform() 메서드로 변환 작업을 수행합니다.
PolynomialFeatures 클래스를 이용해 단항식 $[x_{1}, x_{2}]$를 2차 다항값 $[1, x_{1}, x_{2}, x_{1}^{2}, x_{1}x_{2}, x_{2}^{2}]$로 변환하는 예제입니다.

이렇게 변환된 Polynomial 피처에 선형 회귀를 적용해 다항 회귀를 구현할 수 있습니다. PolynomialFeatures 클래스가 단항식 값을 다항식 값으로 변환해준다는 것을 알아봤습니다. 이번에는 3차 다항 계수를 이용해 3차 다항 회귀 함수식을 PolynomialFeatures와 LinearRegression 클래스를 이용해 구현해봅시다.
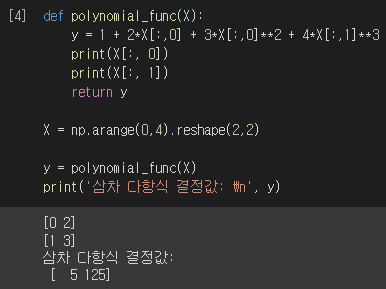
먼저 우리가 예측하고자 하는 실제 3차 다항 결정 함수식을 $y = 1 + 2x_{1} + 3x_{1}^{2} + 4x_{2}^{3}$로 설정했습니다. 해당 함수는 3차 다항 계수 피처 값이 입력되면 결정 값을 반환합니다.

1차 다항식 계수를 3차 다항식 계수로 변환하고, 이를 선형 회귀에 적용하면 다향 회귀가 구현됩니다. PolynomialFeatures(degree=3)은 단항 계수 피처 $[x_{1}, x_{2}]$를 3차 다항 계수 $[1, x_{1}, x_{2}, x_{1}^{2}, x_{1}x_{2}, x_{2}^{2}, x_{1}^{3}, x_{1}^{2}x_{2}, x_{1}x_{2}^{2}, x_{1}^{3}]$와 같이 10개의 다항 계수로 변환합니다.
일차 단항식 계수 피처는 2개였지만, 3차 다항식 계수로 변환하면서 피처의 개수가 10개로 늘어났습니다. 그러므로 여기에 선형 회귀를 적용한다면 회귀 계수가 10개로 늘어납니다. 학습 된 결과 회귀 계수는 정답 함수인 $[1, 2, 0, 3, 0, 0, 0, 0, 0, 4]$와는 약간의 차이가 있지만, 다항 회귀를 통한 근사를 하고 있음을 알 수 있습니다.
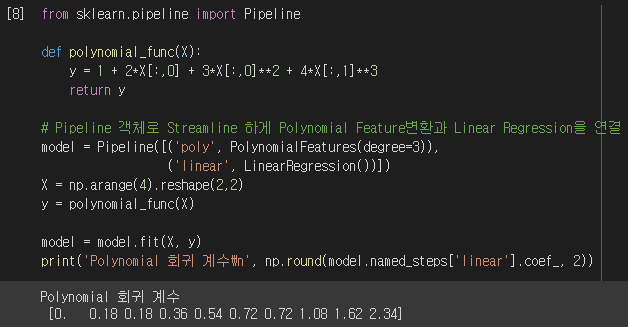
방금 예제와 같이 피처 변환과 선형 회귀 적용을 별도로 처리하는 것보다, 사이킷런의 Pipeline 객체를 이용해 두 과정을 합쳐서 한 번에 다항 회귀를 구현하는 것이 더 명료한 코드입니다. Pipeline을 구성하는 세부 객체에 접근하는 named_steps['객체명']을 이용하여 선형 회귀 모델의 회귀 계수를 확인할 수 있습니다.
다항 회귀는 피처의 직선적 관계가 아닌 복잡한 다항 관계를 모델링할 수 있습니다. 다항식의 차수가 높아질수록 매우 복잡한 피처 간의 관계까지 모델링 가능합니다. 하지만 차수를 높일수록 학습 데이터에만 너무 맞춰진 학습이 이루어져 과적합 문제가 크게 발생합니다.
사이킷런 홈페이지에서 다항 회귀에서의 과소적합과 과적합 문제를 잘 보여주는 예시를 제시합니다.

피처와 y값이 각각 1개인 데이터 세트를 만들어봅시다. y값은 코사인 함수값에 약간의 노이즈가 추가된 값이며, 피처(x)는 0 ~ 1사이에서 30개의 임의로 샘플링한 값입니다. 해당 함수를 다항 회귀를 통해 예측할 것입니다. 이 때 다항 회귀의 차수를 변화시키면서 그에 따른 회귀 예측 곡선과 예측 정확도를 비교해봅시다.
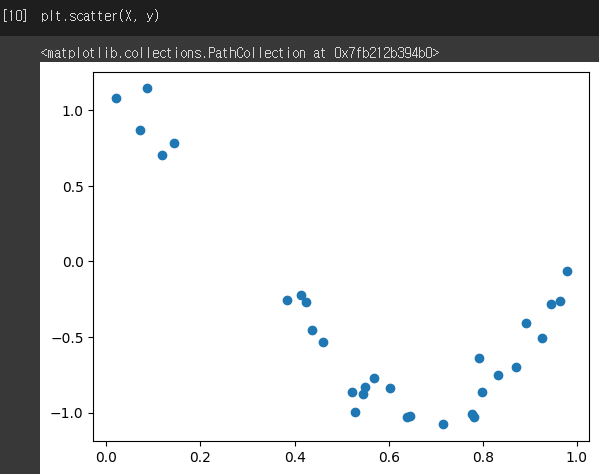
피처에 해당하는 y값을 시각화한 그래프입니다.

다항식 차수를 각각 1, 4, 15로 변경하면서 다항 회귀의 학습을 수행한 뒤 cross_val_score()로 MSE 값을 구해 차수별 예측 성능을 평가합니다. 그리고 0 ~ 1 사이에 균일하게 구성된 100개의 테스트용 데이터 세트를 이용해 차수별 회귀 예측 곡선을 그려보겠습니다.
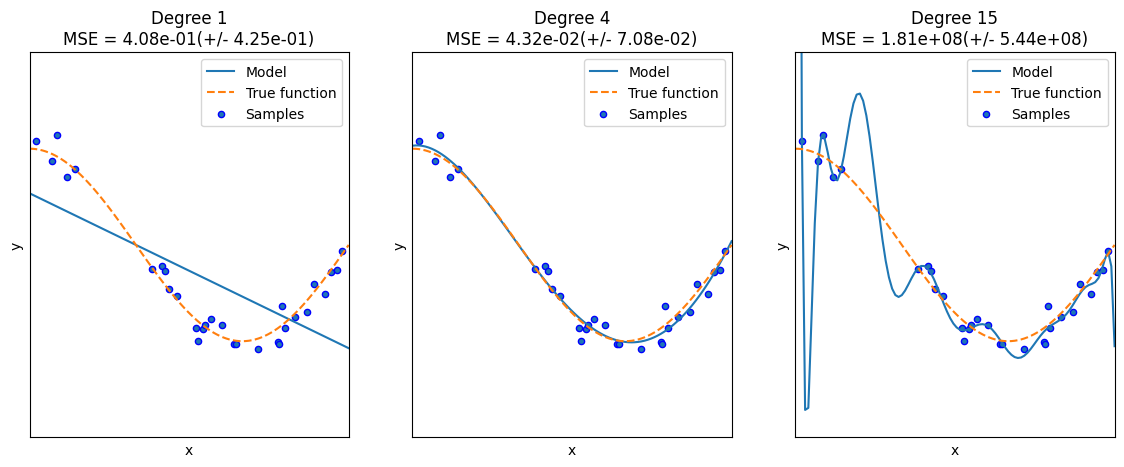
차수가 1인 단순 선형 회귀 모델의 경우 실제 데이터 세트를 예측하기에는 너무 단순해 보입니다. 예측 곡선이 학습 데이터의 패턴을 제대로 반영하지 못하고 있는 과소적합 모델이 되었습니다.
차수가 4인 다항 회귀 모델의 예측 곡선은 실제 데이터 세트의 패턴을 잘 반영하는 것으로 보입니다. 변동하는 잡음까지는 예측하지 못하지만, 전체 패턴을 잘 학습했습니다. MSE도 가장 낮습니다.
차수가 15인 다항 회귀 모델의 경우 MSE값이 매우 큰 것을 볼 수 있습니다. 데이터 세트의 변동 잡음까지 지나치게 반영한 결과 실제 곡선과는 전혀다른 형태의 예측 곡선이 만들어졌습니다. 결과적으로 학습 데이터에만 지나치게 치우친 과적합 모델이 되었습니다.

차수가 15인 경우 회귀 계수 값이 지나치게 큰 값임을 볼 수 있습니다. 15차라는 복잡한 다항식을 만족하기 위해 회귀 계수를 맞추다보니 현실과 너무 동떨어진 예측 결과를 생성합니다.
편향-분산 트레이드오프는 머신러닝이 극복해야 할 중요한 이슈입니다. 차수가 1인 모델은 매우 단순화된 모델로서 한방향으로 지나치게 치우진 경향이 있습니다. 이런 모델을 고편향(High Bias)성을 가졌다고 합니다. 반면 차수가 15인 모델은 개별 학습 데이터의 특성까지 하나하나 반영하면서 매우 복잡한 모델이 되었고, 지나치게 높은 변동성을 가지게 되었습니다. 이런 모델을 고분산(High Variance)성을 가졌다고 합니다.

위의 양궁 과녁 그림은 편향과 분산의 의미를 직관적으로 잘 나타내고 있습니다. 상단 왼쪽의 저편향/저분산 예측 결과가 실제 결과에 매우 잘 근접하면서도 예측 변동이 크지 않고 특정 부분에 집중돼 있는 아주 뛰어난 성능을 보여줍니다. 상단 오른쪽의 저편향/고분산은 예측 결과가 실제 결과에 비교적 근접하지만, 예측 결과가 실제 결과를 중심으로 꽤 넓은 부분에 분포돼 있습니다. 하단 왼쪽의 고편향/저분산은 정확한 결과에서 벗어나면서도 예측이 특정 부분에 집중돼 있습니다. 하단 오른쪽의 고편향/고분산은 정확한 예측 결과를 벗어나면서도 넓은 부분에 분포돼 있습니다.
일반적으로 편향과 분산은 한쪽이 높으면 한쪽이 낮아지는 트레이드 오프 관계를 가집니다.

위의 그림은 편향과 분산의 관계에 따른 전체 오류값(Total Error)의 변화를 잘 보여줍니다. 편향을 낮추고 분산을 높이면서 전체 오류가 가장 낮아지는 골디락스 지점을 통과하면서 분산을 지속적으로 높이면 전체 오류 값이 다시 증가하면서 예측 성능이 저하됩니다. 편향이 높고 분산이 낮은 그래프의 왼쪽 부분의 모델은 과소적합, 편향이 낮고 분산이 높은 그래프의 오른쪽 부분은 과적합을 의미합니다.
편향과 분산이 서로 트레이드 오프를 이루면서 전체 Cost 값이 최대로 낮아지는 모델을 구축하는 것이 가장 효과적인 머신러닝 모델을 만드는 방법입니다.
'파이썬 머신러닝 완벽 가이드' 카테고리의 다른 글
| 파이썬 머신러닝 완벽 가이드 : 선형 회귀 모델을 위한 데이터 전처리 (0) | 2023.05.12 |
|---|---|
| 파이썬 머신러닝 완벽 가이드 : 규제 선형 모델 - 릿지, 라쏘, 엘라스팃넷 (0) | 2023.05.12 |
| 파이썬 머신러닝 완벽 가이드 : 사이킷런 회귀 클래스를 이용한 보스턴 주택 가격 예측 (0) | 2023.05.11 |
| 파이썬 머신러닝 완벽 가이드 : 회귀(Regression) (0) | 2023.05.10 |
| 파이썬 머신러닝 완벽 가이드 : 스태킹 앙상블 (0) | 2023.05.07 |
